


In 1704 the great Isaac Newton described in Opticks, using drawings and words, multiple-prism dispersion [1]. In 1813 Brewster introduced compensating prism pairs for beam expansion [2].
In 1982 physicists working on narrow-linewidth tunable lasers, incorporating multiple-prism grating assemblies, derived a generalized multiple-prism grating dispersion equation [3]. The generalized multiple-prism dispersion equation is the first derivative of the generalized prismatic refraction:
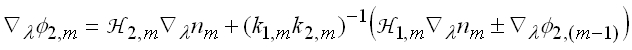
A pedagogical description of these equations is also available [4]. In 1987 the second generalized derivative of the multiple-prism refraction (first derivative of the dispersion) was introduced as a design tool for multiple-prism pulse compressors used in femtosecond lasers [5]. Over the years these equations have been successfully used in pulse compression calculations [6] and as a tool in the design of narrow-linewidth prismatic laser oscillators [7]. Additional applications include laser microscopy.
Multiple-prism beam expanders and arrays were described in matrix form in 1989 [8]. The multiple-prism dispersion theory was given in 4 X 4 matrix form in 1992 [9]. These matrix equations are applicable either to prism pulse compressors or multiple-pism beam expanders. These matrix results are nicely reviewed and summarized in Tunable Laser Optics [10]. Also, in 1992 the cavity linewidth equation was derived using quantum principles [11]. This 1992 paper [11], reported for the first time on the nexus between quantum mechanics principles and classical angular dispersion as expressed via the generalized multiple-prism grating dispersion theory. In 1997, Snell's law (or the law of rafraction) was derived using quantum mechanical interferometric principles [12] and in 2006 this derivation was extended to negative refraction [13]. Certainly, these principles also apply to the generalized description of angular dispersion as shown in [12, 13].
Recently, Duarte has elegantly constructed a theoretical framework that allows the evaluation of higher generalized derivatives, of multiple-prism dispersion, at will [14-16]. These higher derivatives can be used to refine the design of multiple-prism pulse compressors and should find further applications in nonlinear optics [15, 16]. On the other hand, this theoretical framework, provides an elegant, and complete, mathematical description of the prismatic arrays first outlined by Newton’s vision more than 300 years ago. An updated review on this subject is given in [15].
The multiple-prism dispersion theory has also been appled to quantify the angular dispersion in Amici prisms, also known as compound prisms [16]. A review of applicatons of the multiple-prism dispersion theory to laser optics, pulse compression, astronomy, metrology, microscopy, and scientic instrumentation is given in [17].
.jpg)
Multiple-prism array as described by Newton in his Opticks.

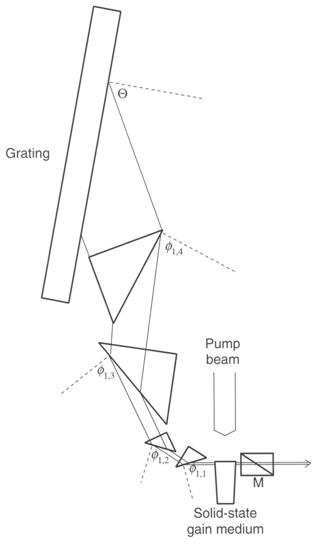
Multiple-prism grating tunable laser oscillator (from Duarte et al. (1998) [19]).






Page published on the 18th of August, 2009
Updated on the 30th of September, 2016